Jos Coenen's blog

De kids zijn met techniek bezig met overbrengingen.
Dat kan ik nog begrijpen en deze Belg ook:
http://users.telenet.be/maartenverhulst/Mainpage.htm

En dan zeggen dat alle Belgen dom zijn, mooi niet!

Wat kan ik me soms (?!) toch dom voelen.
Ooit gehoord van Hamilton?
Nee? Ik ook niet.
Wikipedia wel: http://nl.wikipedia.org/wiki/Hamiltonformalisme

Afleiding uit het Lagrangeformalisme

Stel dat we een mechanisch systeem hebben dat beschreven wordt door het Lagrangeformalisme. De toestand van het systeem op elk moment wordt gegeven door een stel gegeneraliseerde coördinaten 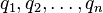$q_1,q_2,\ldots,q_n$ en de bijbehordende gegeneraliseerde snelheden $\dot q_1,\dot q_2,\ldots,\dot q_n$ . In het vervolg van dit artikel zullen ook de tijdsafgeleiden van andere natuurkundige grootheden met een punt worden aangegeven.

De verandering van het systeem in de tijd wordt gegeven door de Euler-Lagrangevergelijkingen,

$\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial L}{\partial\dot q_i}\right)-\frac{\partial L}{\partial q_i}=0\quad(i=1,2,\ldots,n).$

Hierin is $L(q_1,\ldots,q_n,\dot q_1,\ldots,\dot q_n,t)$ de Lagrangiaan van het systeem. We introduceren nu voor elke coördinaat $q i$ de gegeneraliseerde impuls $p i$ geassocieerd met $q i$ door middel van

$p_i=\frac{\partial L}{\partial\dot q_i}.$

Verder voeren we de Hamiltoniaan of Hamiltonfunctie in:

$H(q_1,\ldots,q_n,p_1,\ldots,p_n,t) = \sum_{i=1}^n p_i\dot q_i - L(q_1,\ldots,q_n,\dot q_1,\ldots,\dot q_n,t),$

waarbij we de genereraliseerde snelheden $\dot q_i$ uitdrukken in de variabelen $q_1,\ldots,q_n,p_l,\ldots,p_n,t$ . Vervolgens berekenen we de totale differentiaal van de Hamiltoniaan met behulp van de productregel en de kettingregel:

$\mathrm{d}H = \sum_{i=1}^n\left(p_i\,\mathrm{d}\dot q_i + \dot q_i\,\mathrm{d}p_i - \frac{\partial L}{\partial q_i}\,\mathrm{d}q_i - \frac{\partial L}{\partial\dot q_i}\,\mathrm{d}\dot q_i\right) - \frac{\partial L}{\partial t}\,\mathrm{d}t.$

Vanwege de Euler-Lagrangevergelijkingen en de definitie van $p i$ is dit gelijk aan

$\mathrm{d}H = \sum_{i=1}^n\left(\dot q_i\,\mathrm{d}p_i - \dot p_i\,\mathrm{d}q_i\right) - \frac{\partial L}{\partial t}\,\mathrm{d}t.$

Hieruit volgen de vergelijkingen van Hamilton, ook wel de kanonieke bewegingsvergelijkingen genoemd:

$\dot q_i=\frac{\partial H}{\partial p_i},\qquad\dot p_i=-\frac{\partial H}{\partial q_i}\qquad(i=1,2,\ldots,n).$

Verder is de tijdsafgeleide van $H$ zelf gelijk aan

$\dot H=\frac{\partial H}{\partial t}=-\frac{\partial L}{\partial t}.$

Deze vergelijkingen geven de verandering in de tijd van respectievelijk de plaatscoördinaten, de bijbehorende gegeneraliseerde impulsen en de Hamiltoniaan van het systeem (die in veel gevallen geïdentificeerd kan worden met de energie).

Nou, nou, wie kan hier koffie van maken?
En dan zeggen sommigen dat mijn Java code ingewikkeld dan wel erg abstract is.

ClustrMaps

Jos Coenen's blog

Wednesday, March 28, 2007

Afleiding uit het Lagrangeformalisme

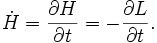
1 comment:

Blog Archive